Wat is de correlatiecoëfficiënt?
Correlatiecoëfficiënt wordt gebruikt om te bepalen hoe sterk de relatie is tussen twee variabelen en de waarden kunnen variëren van -1,0 tot 1,0, waarbij -1,0 een negatieve correlatie vertegenwoordigt en +1,0 een positieve relatie. Het houdt rekening met de relatieve bewegingen in de variabelen en bepaalt vervolgens of er een relatie tussen is.
Formule voor correlatiecoëfficiënten
r = n (∑xy) - ∑x ∑y / √ (n * (∑x 2 - (∑x) 2 )) * (n * (∑y 2 - (∑y) 2 ))
Waar
- r = correlatiecoëfficiënt
- n = aantal waarnemingen
- x = 1 e variabele in de context
- y = 2e variabele
Uitleg
Als er een correlatie is, of zeg maar de relatie tussen twee variabelen, dan zal het aangeven of een van de variabelen in waarde verandert, dan zal de andere variabele ook de neiging hebben om in waarde te veranderen, zeg specifiek die in dezelfde of in de andere kant. Het tellergedeelte van de vergelijking voert een test uit en de relatieve sterkte van de variabelen die samen bewegen, en het noemergedeelte van de vergelijking schaalt de teller door de verschillen tussen de variabelen en gekwadrateerde variabelen te vermenigvuldigen.
Voorbeelden
Voorbeeld 1
Beschouw de volgende twee variabelen, x en y, u moet de correlatiecoëfficiënt berekenen.
Hieronder vindt u gegevens voor de berekening.

Oplossing:
Met behulp van de bovenstaande vergelijking kunnen we het volgende berekenen

We hebben alle waarden in de bovenstaande tabel met n = 4.
Laten we nu de waarden invoeren voor de berekening van de correlatiecoëfficiënt.

Daarom is de berekening als volgt,

r = (4 * 25.032,24) - (262,55 * 317,31) / √ ((4 * 20.855,74) - (262,55) 2 ) * ((4 * 30.058,55) - (317,31) 2 )
r = 16.820,21 / 16.831,57
De coëfficiënt is -

Coëfficiënt = 0,99932640
Voorbeeld 2
Land X is een land met een groeiende economie en wil een onafhankelijke analyse maken van de beslissingen die zijn centrale bank neemt met betrekking tot renteveranderingen, of deze de inflatie hebben beïnvloed en of de centrale bank in staat is om deze te controleren.
Hieronder volgt het overzicht van het rentepercentage en het inflatiepercentage dat in die jaren gemiddeld in het land heerste.
Hieronder vindt u gegevens voor de berekening.

De president van het land heeft u benaderd om een analyse uit te voeren en daarover in de volgende vergadering een presentatie te geven. Gebruik correlatie en bepaal of de centrale bank haar doel heeft bereikt of niet.
Oplossing:
Met behulp van de hierboven besproken formule kunnen we de correlatiecoëfficiënt berekenen. Rentevoet behandelen als één variabele, bijvoorbeeld x, en inflatie als een andere variabele behandelen als y.

We hebben alle waarden in de bovenstaande tabel met n = 6.
Laten we nu de waarden invoeren voor de berekening van de correlatiecoëfficiënt.


r = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
r = -5,36 / 5,88
De correlatie zal zijn -

Correlatie = -0,92
Analyse: Het lijkt erop dat de correlatie tussen de rente en de inflatie negatief is, wat de juiste relatie lijkt te zijn. Naarmate de rente stijgt, daalt de inflatie, wat betekent dat ze de neiging hebben om in de tegenovergestelde richting van elkaar te bewegen, en uit het bovenstaande resultaat blijkt dat de centrale bank erin geslaagd is het besluit met betrekking tot het rentebeleid te implementeren.
Voorbeeld # 3
Laboratorium ABC doet onderzoek naar lengte en leeftijd en wilde weten of er een relatie tussen is. Ze hebben voor elk van de categorieën een steekproef van 1000 mensen verzameld en kwamen tot een gemiddelde lengte in die groep.
Hieronder worden gegevens gegeven voor de berekening van de correlatiecoëfficiënt.

U moet de correlatiecoëfficiënt berekenen en tot de conclusie komen dat er een verband bestaat.
Oplossing:
Leeftijd behandelen als één variabele, zeg x, en hoogte (in cm) behandelen als een andere variabele als y.

We hebben alle waarden in de bovenstaande tabel met n = 6.
Laten we nu de waarden invoeren voor de berekening van de correlatiecoëfficiënt.

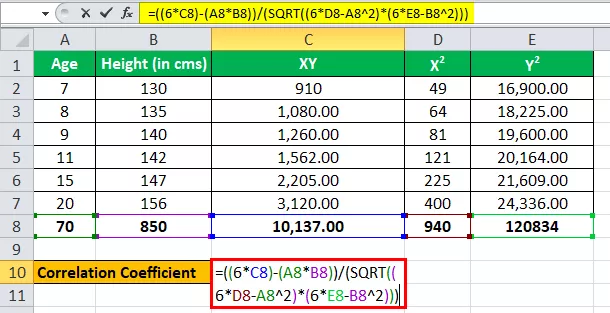
r = (6 * 10.137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1,20.834) - (850) 2 )
r = 1.322,00 / 1.361,23
De correlatie zal zijn -

Correlatie = 0.971177099
Relevantie en gebruik
Het wordt in de statistieken voornamelijk gebruikt om de sterkte van de relatie tussen de variabelen die worden overwogen te analyseren en verder meet het ook of er een lineair verband bestaat tussen de gegeven gegevenssets en hoe goed ze kunnen worden gerelateerd. Een van de meest voorkomende maten die bij correlatie worden gebruikt, is de Pearson-correlatiecoëfficiënt.
Als een variabele in waarde verandert en samen met die andere variabele in waarde verandert, is het van cruciaal belang die relatie te begrijpen, aangezien men de waarde van de eerste variabele kan gebruiken om de verandering in de waarde van de laatste variabele te voorspellen. Een correlatie heeft tegenwoordig veel meervoudige toepassingen in dit moderne tijdperk, zoals het wordt gebruikt in de financiële sector, wetenschappelijk onderzoek, en waar niet. Maar het is belangrijk om te weten dat correlatie drie belangrijke soorten relaties heeft. De eerste is een positieve relatie, die aangeeft dat als er een verandering in de waarde van een variabele is, er een verandering in de gerelateerde variabele in dezelfde richting zal plaatsvinden. Evenzo, als er een negatieve relatie is, zal de gerelateerde variabele zich in de tegenovergestelde richting gedragen. Ook als er geen correlatie is, zal r een nulwaarde impliceren.Bekijk de onderstaande afbeeldingen om het concept beter te begrijpen.









