Negatieve correlatie-definitie
In lekentermen is negatieve correlatie een relatie tussen twee variabelen. Ze maken deel uit van een functie waarin afhankelijke en onafhankelijke variabelen in waarde in verschillende richtingen bewegen. Als de onafhankelijke variabele bijvoorbeeld toeneemt, neemt de afhankelijke variabele af, en vice versa.
Negatieve correlatie kan worden beschreven door de correlatiecoëfficiënt wanneer de waarde van deze correlatie tussen 0 en -1 ligt. Het bedrag van een perfecte negatieve correlatie is -1. De sterkte van de correlatie tussen de variabelen kan variëren. Stel dat twee variabelen, x en y, correleren met -0,8. Dit betekent dat als x met 1 eenheid toeneemt, y met 0,8 afneemt. Bedenk nu dat de negatieve correlatie tussen deze variabelen -0,1 is. In dit geval zal elke eenheidsverandering in de waarde van variabele x resulteren in een verschil van 0,1 eenheid alleen in de kosten van variabele y.
Negatieve correlatie begrijpen
Om de negatieve correlatie beter te begrijpen, moeten we ook een basiskennis hebben van correlatie. Correlatie is een statistisch hulpmiddel dat een maat is voor de mate van relatie tussen twee verschillende functies. Bijvoorbeeld het gewicht en de lengte van een persoon. Over het algemeen neemt de waarde van de persoon toe naarmate de lengte toeneemt. Het geeft aan dat er een positieve correlatie bestaat tussen lengte en gewicht, omdat naarmate de ene variabele toeneemt, ook andere variabelen toenemen. Maar de correlatie is negatief als de twee variabelen in tegengestelde richtingen bewegen, bijvoorbeeld de hoogte vanaf het afdichtingsniveau en de temperatuur. Naarmate de hoogte toeneemt, neemt de temperatuur af.
De formule geeft correlatie:

Hier,
- r = correlatiecoëfficiënt;
- = Gemiddelde van variabele X;
- = Gemiddelde van variabele Y
Herschikken geeft ons deze formule:

Correlatie kan elke waarde tussen -1 en 1 aannemen. Het minteken geeft een negatieve correlatie aan, terwijl een positief teken een positieve correlatie aangeeft. Nulcorrelatie betekent dat er geen verband is tussen de twee variabelen.

Waarom is een negatieve correlatie belangrijk?
- Portfoliomanagement : correlatie wordt veel gebruikt bij het beheer van de portefeuilles. Er wordt vaak gezegd dat portefeuilles divers moeten zijn. Het moet bestaan uit meerdere investeringen met verschillende risico's en opbrengsten. Als we hetzelfde type effecten in onze portefeuille hebben, heeft elke belangrijke gebeurtenis niet alleen gevolgen voor één effect, maar voor de hele portefeuille. Daartoe vinden we een verband tussen de rendementen van effecten. De deposito's met perfect positieve correlaties mogen niet samen worden gekocht. Om de portefeuille te diversifiëren, worden vaak de inzetten met negatieve correlaties toegevoegd. Beschouw het hierboven besproken voorbeeld van aandelen van luchtvaartmaatschappijen en olieprijzen. Als een portefeuille energieaandelen heeft, kan het management overwegen aandelen van luchtvaartmaatschappijen te kopen om zich in te dekken tegen de daling van de olieprijzen.
- Economie : veel trends die verband houden met economie hebben te maken met een negatieve correlatie. Deze relatie tussen de bewegingen kan nuttig zijn voor zaken die betrekking hebben op het economisch beleid. Bijvoorbeeld werkloosheid en consumentenuitgaven. Wat betreft de stijgende uitgaven, daalt de werkloosheid (in het algemeen).
Real-life voorbeelden van negatieve correlatie
- Olieprijzen en voorraden van luchtvaartmaatschappijen: olie is een belangrijke grondstof voor luchtvaartmaatschappijen. Naarmate de olieprijzen stijgen, begint hun winstgevendheid te dalen, wat ook tot uiting komt in hun aandelenkoersen. Daarom vertonen ze een negatieve correlatie
- Aandelenmarkt en goudprijzen (meestal, niet altijd): Goud fungeert altijd als een alternatieve investeringsoptie voor aandelenbeleggers. Dus wanneer de aandelenmarkt lijkt te dalen, raken beleggers geïnteresseerd in beleggen in goud en dus beginnen de goudprijzen te stijgen.
Praktisch voorbeeld van negatieve correlatie
Stel dat twee aandelen in de periode 2011-16 jaarlijks de volgende rendementen hebben opgeleverd:

Beschouw het aandelenrendement van het eerste aandeel als variabele 'x' en dat van het tweede aandeel als 'y'.
Berekening van variabele xy
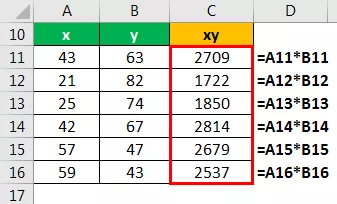
Berekening van variabele X 2

Berekening van variabele Y 2

Som

Berekening van correlatiecoëfficiënt (r)

- = ((6 * 14311) - (247 * 376)) / (((6 * 11409) - (247 2)) 0,5 * ((6 * 247160- (376 2)) 0,5)
- = Correlatiecoëfficiënt (r) = -0,97608
Raadpleeg het bovenstaande Excel-blad voor een gedetailleerde berekening.
De negatieve waarde van de correlatiecoëfficiënt laat zien dat de variabelen negatief gecorreleerd zijn.
Conclusie
Soms zijn er andere factoren die ervoor zorgen dat de variabelen zich op een bepaalde manier gedragen. In het hierboven besproken voorbeeld kan worden afgeleid dat wanneer x toeneemt, y afneemt. Maar het is verkeerd om te veronderstellen dat de stijging van 'x' ervoor zorgt dat de 'y' afneemt, omdat het mogelijk is dat beide betrokken bedrijven betrokken zijn bij totaal verschillende activiteiten en worden beïnvloed door verschillende economische omstandigheden.
Daarom mogen correlaties alleen worden gebruikt om een oorzaak vast te stellen. De leidinggevenden kunnen het gebruiken om de relatie tussen variabelen, zoals marktvraag en consumentenbestedingen, te begrijpen die al bestaat als onderdeel van de analyse. Maar het mag niet worden gebruikt om de verandering in een variabele als gevolg van andere variabelen te onderzoeken, omdat er altijd meerdere factoren zullen zijn die die relatie beïnvloeden. Bijvoorbeeld consumentenuitgaven in de markt en inkomsten van een FMCG-bedrijf. Ze vertonen misschien een positieve correlatie, maar het is mogelijk dat de inkomsten van dat bedrijf zijn gestegen vanwege een andere reden, zoals de lancering van een nieuw product of uitbreiding naar een opkomende economie.








