PV = L * (1 - (1 + r) -n / r)
Waarin,- PV is de huidige waarde van het uitstaande saldo
- L is de bestaande betaling
- r is de rentevoet
- n is de frequentie van betalingen
Calculator voor uitbetaling van schulden
Schuldbetalingscalculator is een soort rekenmachine waarbij als de lener de uitstaande leningen wil consolideren en proberen ze snel af te betalen om de rentelast en overtollige uitstroom te verminderen.
Over de calculator voor het afbetalen van schulden
Zoek eerst de contante waarde van de uitstaande saldi op de meerdere leningen.
PV = L * (1 - (1 + i) -n / r)Het volgende zou zijn om het nieuwe termijnbedrag te weten te komen, dat ofwel de som van het bestaande termijnbedrag en eventueel nog te betalen aanvullende betaling kan zijn.
Bereken nu de termijn waarbinnen de schuld kan worden afbetaald
nPVA = ln ((1 - PV (i) / L ') -1) ) / ln (1 + i)Waarin,
- PV is de huidige waarde van het uitstaande saldo
- L is de bestaande betaling
- L 'is de nieuwe betaling
- i is de rentevoet
- n is de frequentie van betalingen
- nPVA is het aantal periodieke betalingen
Het is een handige rekenmachine omdat het berekent wat de ambtstermijn zal zijn als alle schulden zijn afbetaald. In dit geval kan de lener zitten met meerdere leningen met verschillende rentetarieven en is hij bereid deze te consolideren. Verder kan de lener zelfs het afbetalingsbedrag periodiek willen verhogen of het afbetalingsbedrag ook willen consolideren. Dit zal hem helpen bij het verminderen van de rentelast en ook bij het vervroegd aflossen van schulden. De beslissing is niet zo eenvoudig als nodig was om het afbetalingsbedrag te verhogen, wat de kasstroom van de kredietnemer zou kunnen verhogen. Deze calculator helpt alleen om te berekenen binnen welke tijdsspanne ze de schuld volledig kunnen afbetalen wanneer de schulden worden geconsolideerd.
Hoe te berekenen met behulp van de calculator voor het afbetalen van schulden?
Men moet de onderstaande stappen volgen om te berekenen dat de duur van de geconsolideerde schuld loont.
Stap # 1 - Ten eerste moet de lener bepalen wat het huidige uitstaande saldo van de schuld is, wat niets anders is dan het achterhalen van de huidige waarde van de schuld.
Stap # 2 - Bepaal nu het nieuwe termijnbedrag, dat is de som van het bestaande termijnbedrag dat hij momenteel betaalt en het extra bedrag waarmee de lener denkt te beginnen.
Stap # 3 - Ontdek de lening, die hoger rentedragend is en maak duidelijk dat de schuld eerst loont en doorgaat met het betalen van het minimum- of afbetalingsbedrag voor andere uitstaande leningen.
Stap # 4 - Bereken nu de uitstaande hoofdsom van de resterende leningen en bereken de looptijd van de lening met het nieuwe afbetalingsbedrag.
Stap # 5 - De resulterende ambtstermijn kan worden omgezet in jaren door de waarde die in stap 4 is verkregen te delen door 12 en cijfers aan de rechterkant van de komma kunnen worden vermenigvuldigd met 12 om ze in maanden te krijgen.
Voorbeeld
Meneer X heeft twee uitstaande leningen, een autolening en een andere hypothecaire lening.
De details van beide leningen worden hieronder gegeven:

De filiaalmanager heeft de heer X benaderd met een regeling waarbij hij de lopende leningen kan consolideren en schulden vervroegd kan aflossen. De bankier verstrekte hem de details van de regeling die eerst de hogere schuld moesten afbetalen en vervolgens het vaste bedrag van de afgeloste lening op de hypotheeklening zouden voortzetten, wat zijn ambtstermijn van leningafsluiting zou verminderen. De heer X stemde er ook mee in om het afbetalingsbedrag met $ 200 te verhogen terwijl de uitstaande leningen worden geconsolideerd en zal dit blijven doen totdat de schulden zijn afbetaald.
U moet de ambtstermijn berekenen waarmee de schuld zal worden afbetaald.
Oplossing:
We moeten de huidige waarde van het huidige openstaande schuldsaldo berekenen, dat kan worden berekend met de onderstaande formule:
Autolening
Rentepercentage op maandbasis = 8/12 = 0,67%
De resterende periode is (7 * 12) - (3 * 12), dat is 84 - 36, dat is 48.
PV = L * (1 - (1 + i) -n / r)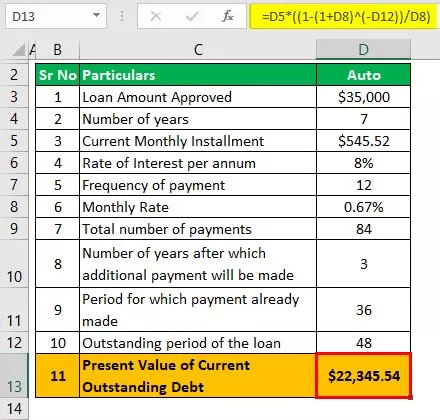
- = $ 545. 52 * (1 - (1 + 0,67%) -48 ) / 0,67%)
- = $ 22.345,54
Hypothecaire lening
Rentepercentage op maandbasis = 5/12 = 0,42%
De resterende periode is (25 * 12) - (10 * 12), dat is 300 - 120, dat is 180.
PV = L * (1 - (1 + i) -n / r)
- = $ 1.227,64 * (1 - (1 + 0,42%) -180 / 0,42%)
- = $ 155.241,51
Geconsolideerde uitstaande lening

- = $ 22.345,44 + $ 155.241,40
- = $ 177.586,84
We krijgen hier te zien dat de bestaande maandelijkse afbetaling die hij betaalt voor een autolening is $ 545,52, en het bestaande afbetalingsbedrag voor een hypothecaire lening is $ 1227,64. Het geconsolideerde termijnbedrag zou $ 1.773,16 zijn, en verder wil de heer X dit bedrag ook met $ 200 verhogen. Daarom zou het totale nieuwe termijnbedrag $ 1.973,16 zijn
Ten eerste zou het afbetalingsbedrag van de autolening worden afbetaald omdat het hogere rentedragend is, en het nieuwe bedrag dat zou worden gebruikt om de autolening af te betalen zou $ 545,52 + $ 200 zijn, wat $ 745,52 is, en het restbedrag zal worden gebruikt om te betalen hypotheeklening die $ 1.973,16 - $ 745,52 is, wat gelijk is aan $ 1.227,64
Nu zullen we berekenen binnen welke tijdspanne autolening zal worden verrekend
nPVA = ln ((1 - PV (i) / L ') -1) ) / ln (1 + i)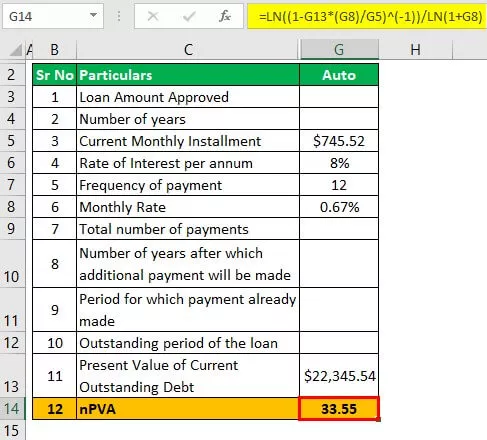
- = ln (((1- 22.345,44 * (0,67%) / 745,52) -1 ) / ln (1 + 0,67%)
- = 33,55
Nu zou de uitstaande ambtsperiode van een hypothecaire lening 180 zijn, verminderd met 33,55, wat 146,45 is
Hypothecaire lening nadat autolening is afbetaald
Rentepercentage op maandbasis = 5/12 = 0,42%
PV = L * (1 - (1 + i) -n / r)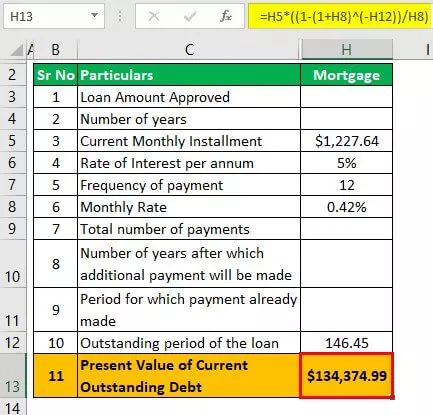
- = $ 1.227,64 * (1 - (1 + 0,42%) -146,45 / 0,42%)
- = $ 134.374,99
Nu zullen we berekenen binnen welke tijdspanne de hypotheeklening zal worden afgelost
nPVA = ln ((1 - PV (i) / L ') -1 ) / ln (1 + i)
- = ln (((1- 134.374,92 * (0,42%) / 1.973,16) -1 ) / ln (1 + 0,42%)
- = 80,26
Daarom is de totale ambtstermijn waarbinnen de lening kan worden verrekend 33,55 + 80,26, wat 113,81 is en wanneer deze wordt gedeeld door 12, wat 9,48 jaar is, is dat in 9 jaar en 6 maanden.








